컬러맵 정규화

기본적으로 컬러맵을 사용하는 객체는 데이터 값 vmin 에서 vmax 까지 컬러맵의 색상을 선형 매핑합니다 . 예를 들어:

pcm = ax.pcolormesh(x, y, Z, vmin=-1., vmax=1., cmap='RdBu_r')

Z 의 데이터 를 -1에서 +1까지 선형으로 매핑하므로 Z=0 은 컬러맵 RdBu_r (이 경우 흰색) 의 중앙에 색상을 제공합니다 .

Matplotlib는 입력 데이터에서 [0, 1]로의 정규화가 먼저 발생한 다음 컬러맵의 인덱스에 매핑되는 두 단계로 이 매핑을 수행합니다. 정규화는 matplotlib.colors()모듈에 정의된 클래스입니다. 기본 선형 정규화는 matplotlib.colors.Normalize()입니다.

데이터를 색상에 매핑하는 아티스트는 인수 vmin 및 vmax 를 전달하여 matplotlib.colors.Normalize()인스턴스를 구성한 다음 호출합니다.

In [1]: import matplotlib as mpl

In [2]: norm = mpl.colors.Normalize(vmin=-1, vmax=1)

In [3]: norm(0)
Out[3]: 0.5

그러나 때때로 데이터를 비선형 방식으로 컬러맵에 매핑하는 것이 유용한 경우가 있습니다.

대수

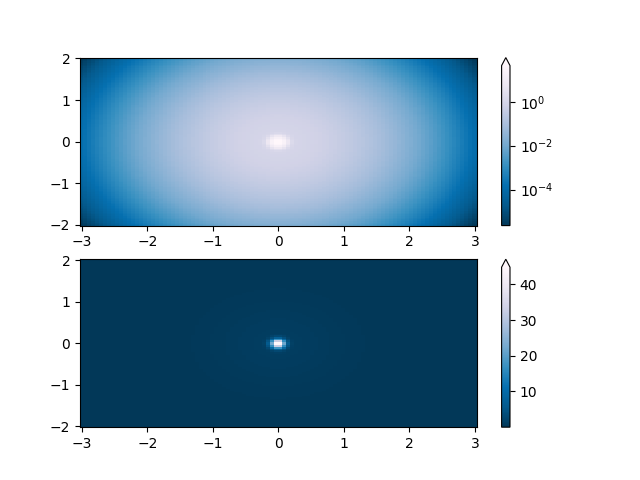
가장 일반적인 변환 중 하나는 로그를 취하여(밑이 10인 경우) 데이터를 플로팅하는 것입니다. 이 변환은 서로 다른 척도에 걸쳐 변경 사항을 표시하는 데 유용합니다. 다음 을 colors.LogNorm통해 데이터를 정규화합니다. \(log_{10}\). 아래 예에는 두 개의 범프가 있는데 하나는 다른 것보다 훨씬 작습니다. 를 사용하면 colors.LogNorm각 범프의 모양과 위치를 명확하게 볼 수 있습니다.

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.cbook as cbook
from matplotlib import cm

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]

# A low hump with a spike coming out of the top right.  Needs to have
# z/colour axis on a log scale so we see both hump and spike.  linear
# scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolor(X, Y, Z,
                   norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
                   cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')

pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
plt.show()

중심

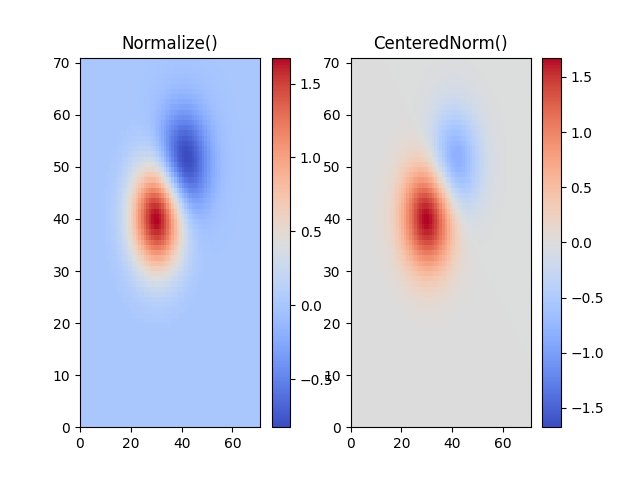
대부분의 경우 데이터는 중심을 중심으로 대칭적입니다. 예를 들어 중심 0 주변의 양수 및 음수 변칙이 있습니다. 이 경우 중심을 0.5에 매핑하고 중심에서 가장 큰 편차가 있는 데이터 포인트를 매핑하려고 합니다. 값이 중심보다 크면 1.0, 그렇지 않으면 0.0입니다. 규범 colors.CenteredNorm은 이러한 매핑을 자동으로 생성합니다. 불포화 색상의 중심에서 만나는 서로 다른 색상 가장자리를 사용하는 발산 색상표와 결합하기에 적합합니다.

대칭 중심이 0이 아닌 경우 vcenter 인수 로 설정할 수 있습니다 . 중앙 양쪽의 대수 스케일링은 colors.SymLogNorm아래를 참조하십시오. 중심 위와 아래에 다른 매핑을 적용하려면 colors.TwoSlopeNorm아래를 사용하십시오.

delta = 0.1
x = np.arange(-3.0, 4.001, delta)
y = np.arange(-4.0, 3.001, delta)
X, Y = np.meshgrid(x, y)
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (0.9*Z1 - 0.5*Z2) * 2

# select a divergent colormap
cmap = cm.coolwarm

fig, (ax1, ax2) = plt.subplots(ncols=2)
pc = ax1.pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax1)
ax1.set_title('Normalize()')

pc = ax2.pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax2)
ax2.set_title('CenteredNorm()')

plt.show()

대칭 로그

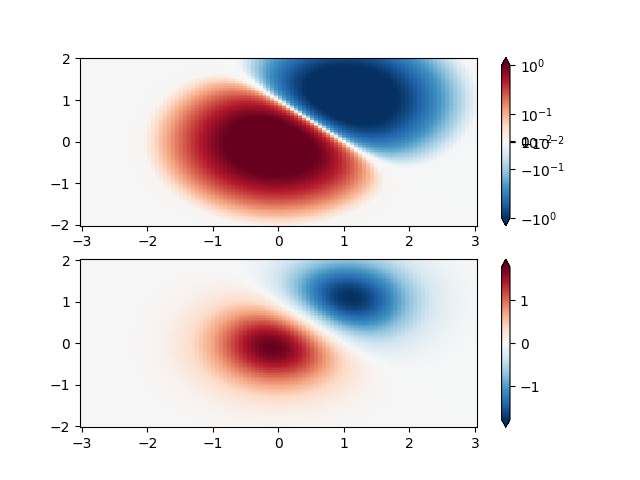
마찬가지로 양수 데이터와 음수 데이터가 있는 경우가 가끔 발생하지만 여전히 두 데이터 모두에 로그 스케일링을 적용하고 싶습니다. 이 경우 음수도 대수적으로 스케일링되고 더 작은 숫자로 매핑됩니다. 예를 들어 이면 vmin=-vmax음수는 0에서 0.5로, 양수는 0.5에서 1로 매핑됩니다.

0에 가까운 값의 로그는 무한대에 가까워지는 경향이 있으므로 0 주변의 작은 범위는 선형으로 매핑해야 합니다. linthresh 매개변수 를 사용하면 사용자가 이 범위(- linthresh , linthresh )의 크기를 지정할 수 있습니다. 컬러 맵에서 이 범위의 크기는 linscale 에 의해 설정됩니다 . linscale == 1.0( 기본값 )인 경우 선형 범위의 양수 및 음수 절반에 사용되는 공간은 대수 범위에서 10단위와 같습니다.

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolormesh(X, Y, Z,
                       norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
                                              vmin=-1.0, vmax=1.0, base=10),
                       cmap='RdBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='both')

pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='both')
plt.show()

멱법칙

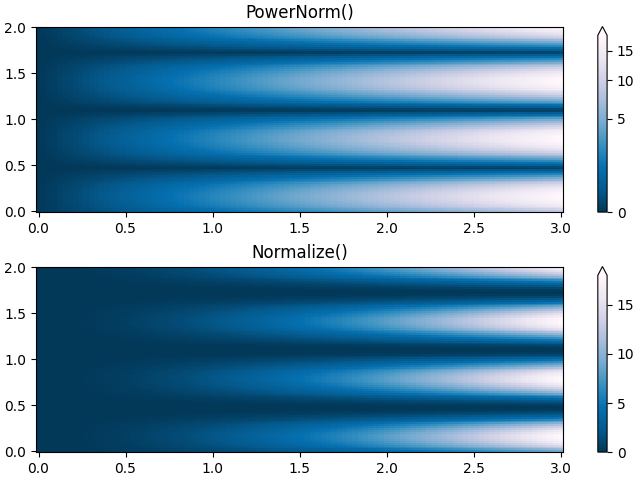
때때로 색상을 거듭제곱 관계로 다시 매핑하는 것이 유용합니다(예:\(y=x^{\gamma}\), 어디\(\gamma\)힘이다). 이를 위해 우리는 colors.PowerNorm. gamma 인수로 사용합니다 ( gamma == 1.0 은 기본 선형 정규화를 생성합니다).

메모

이러한 유형의 변환을 사용하여 데이터를 플로팅하는 데는 타당한 이유가 있을 것입니다. 테크니컬 뷰어는 선형 및 대수 축과 데이터 변환에 사용됩니다. 멱함수 법칙은 덜 일반적이며 시청자는 멱함수 법칙이 사용되었음을 명시적으로 인식해야 합니다.

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2

fig, ax = plt.subplots(2, 1, constrained_layout=True)

pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=0.5),
                       cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')
ax[0].set_title('PowerNorm()')

pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
ax[1].set_title('Normalize()')
plt.show()

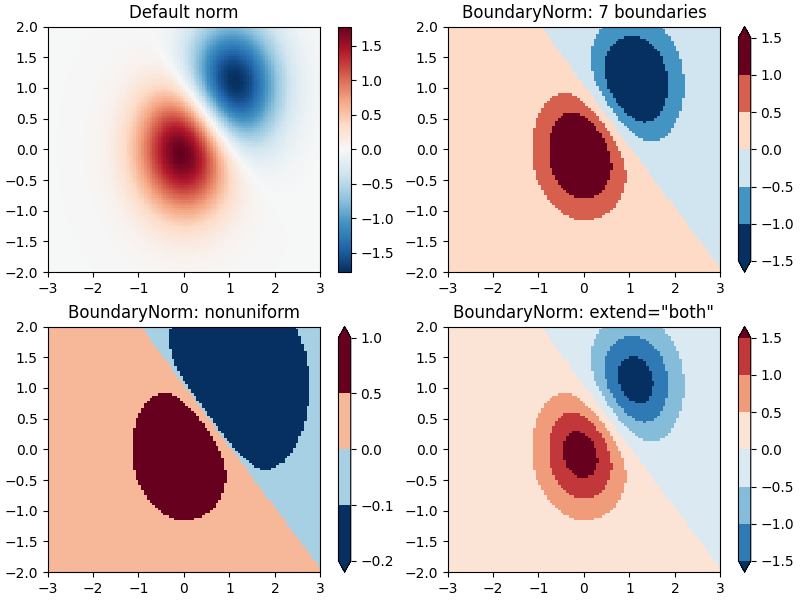
불연속 범위

Matplotlib와 함께 제공되는 또 다른 정규화는 colors.BoundaryNorm. vmin 및 vmax 외에도 매핑할 데이터 사이의 경계를 인수로 사용합니다. 그런 다음 색상은 이러한 "경계" 사이에 선형으로 분포됩니다. 확장 인수를 사용하여 범위를 벗어난 상한 및/또는 하한 값을 색상이 분포되는 범위에 추가 할 수도 있습니다 . 예를 들어:

In [4]: import matplotlib.colors as colors

In [5]: bounds = np.array([-0.25, -0.125, 0, 0.5, 1])

In [6]: norm = colors.BoundaryNorm(boundaries=bounds, ncolors=4)

In [7]: print(norm([-0.2, -0.15, -0.02, 0.3, 0.8, 0.99]))
[0 0 1 2 3 3]

참고: 다른 규범과 달리 이 규범은 0에서 ncolors -1까지의 값을 반환합니다.

N = 100
X, Y = np.meshgrid(np.linspace(-3, 3, N), np.linspace(-2, 2, N))
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = ((Z1 - Z2) * 2)[:-1, :-1]

fig, ax = plt.subplots(2, 2, figsize=(8, 6), constrained_layout=True)
ax = ax.flatten()

# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')

# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')

# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')

# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')
plt.show()

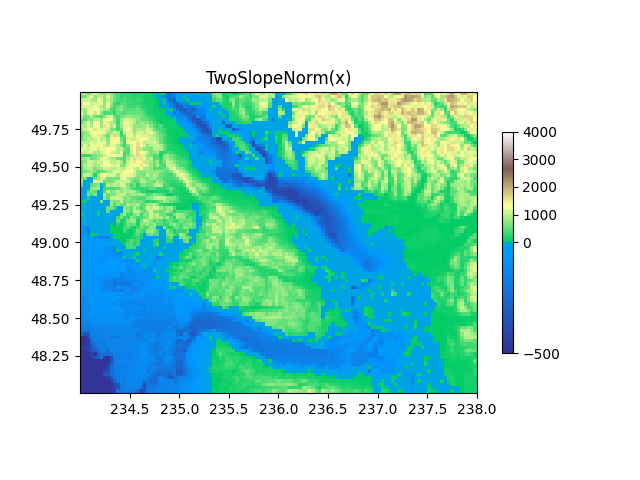
TwoSlopeNorm: 중심의 양쪽에 다른 매핑

때때로 우리는 개념적 중심점의 양쪽에 다른 컬러맵을 갖고 싶고 이 두 컬러맵이 다른 선형 스케일을 갖기를 원합니다. 예를 들어 육지와 바다의 중심이 0인 지형도가 있지만 육지는 일반적으로 물의 깊이 범위보다 육지의 고도 범위가 더 크며 종종 다른 컬러맵으로 표시됩니다.

dem = cbook.get_sample_data('topobathy.npz', np_load=True)
topo = dem['topo']
longitude = dem['longitude']
latitude = dem['latitude']

fig, ax = plt.subplots()
# make a colormap that has land and ocean clearly delineated and of the
# same length (256 + 256)
colors_undersea = plt.cm.terrain(np.linspace(0, 0.17, 256))
colors_land = plt.cm.terrain(np.linspace(0.25, 1, 256))
all_colors = np.vstack((colors_undersea, colors_land))
terrain_map = colors.LinearSegmentedColormap.from_list(
    'terrain_map', all_colors)

# make the norm:  Note the center is offset so that the land has more
# dynamic range:
divnorm = colors.TwoSlopeNorm(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=divnorm,
                    cmap=terrain_map, shading='auto')
# Simple geographic plot, set aspect ratio because distance between lines of
# longitude depends on latitude.
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('TwoSlopeNorm(x)')
cb = fig.colorbar(pcm, shrink=0.6)
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])
plt.show()

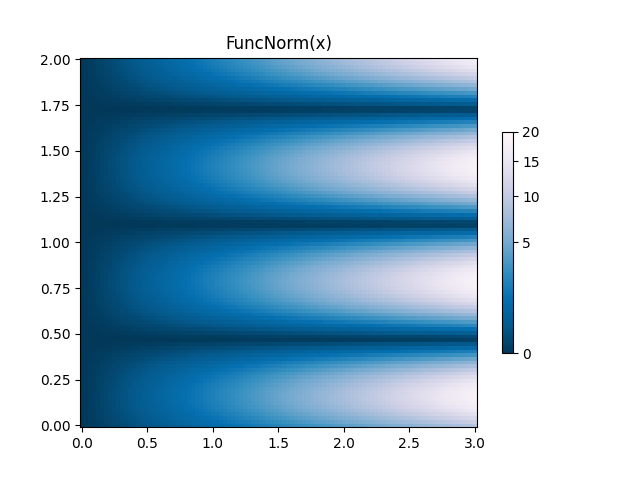
FuncNorm: 임의 함수 정규화

위의 규범이 원하는 정규화를 제공하지 않는 경우 FuncNorm자신만의 정규화를 정의하는 데 사용할 수 있습니다. PowerNorm이 예는 0.5의 거듭제곱과 동일합니다 .

def _forward(x):
    return np.sqrt(x)


def _inverse(x):
    return x**2

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots()

norm = colors.FuncNorm((_forward, _inverse), vmin=0, vmax=20)
pcm = ax.pcolormesh(X, Y, Z1, norm=norm, cmap='PuBu_r', shading='auto')
ax.set_title('FuncNorm(x)')
fig.colorbar(pcm, shrink=0.6)
plt.show()

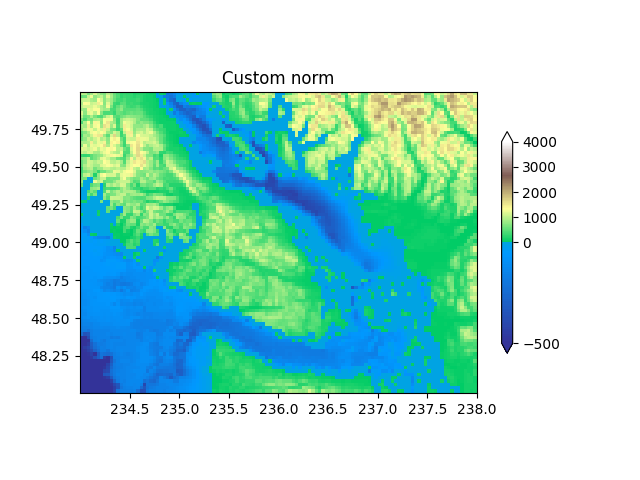
사용자 지정 정규화: 두 개의 선형 범위를 수동으로 구현

위에서 TwoSlopeNorm설명한 내용은 자신의 규범을 정의하는 데 유용한 예입니다. 컬러바가 작동하려면 표준에 대한 반전을 정의해야 합니다.

class MidpointNormalize(colors.Normalize):
    def __init__(self, vmin=None, vmax=None, vcenter=None, clip=False):
        self.vcenter = vcenter
        super().__init__(vmin, vmax, clip)

    def __call__(self, value, clip=None):
        # I'm ignoring masked values and all kinds of edge cases to make a
        # simple example...
        # Note also that we must extrapolate beyond vmin/vmax
        x, y = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1.]
        return np.ma.masked_array(np.interp(value, x, y,
                                            left=-np.inf, right=np.inf))

    def inverse(self, value):
        y, x = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1]
        return np.interp(value, x, y, left=-np.inf, right=np.inf)


fig, ax = plt.subplots()
midnorm = MidpointNormalize(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=midnorm,
                    cmap=terrain_map, shading='auto')
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('Custom norm')
cb = fig.colorbar(pcm, shrink=0.6, extend='both')
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])

plt.show()