중첩 원형 차트 #

다음 예제는 Matplotlib에서 중첩 원형 차트를 작성하는 두 가지 방법을 보여줍니다. 이러한 차트를 종종 도넛형 차트라고 합니다.

import matplotlib.pyplot as plt
import numpy as np

파이 차트를 만드는 가장 간단한 방법은 이 pie방법을 사용하는 것입니다.

이 경우 파이는 그룹의 개수에 해당하는 값을 갖습니다. 먼저 세 그룹에 해당하는 일부 가짜 데이터를 생성합니다. 내부 원에서는 각 번호를 자체 그룹에 속하는 것으로 취급합니다. 외부 원에서 원래 3개 그룹의 구성원으로 표시합니다.

도넛 모양의 효과는 wedgeprops 인수 width를 통해 a를 파이의 쐐기 로 설정하여 얻을 수 있습니다.

fig, ax = plt.subplots()

size = 0.3
vals = np.array([[60., 32.], [37., 40.], [29., 10.]])

cmap = plt.colormaps["tab20c"]
outer_colors = cmap(np.arange(3)*4)
inner_colors = cmap([1, 2, 5, 6, 9, 10])

ax.pie(vals.sum(axis=1), radius=1, colors=outer_colors,
       wedgeprops=dict(width=size, edgecolor='w'))

ax.pie(vals.flatten(), radius=1-size, colors=inner_colors,
       wedgeprops=dict(width=size, edgecolor='w'))

ax.set(aspect="equal", title='Pie plot with `ax.pie`')
plt.show()

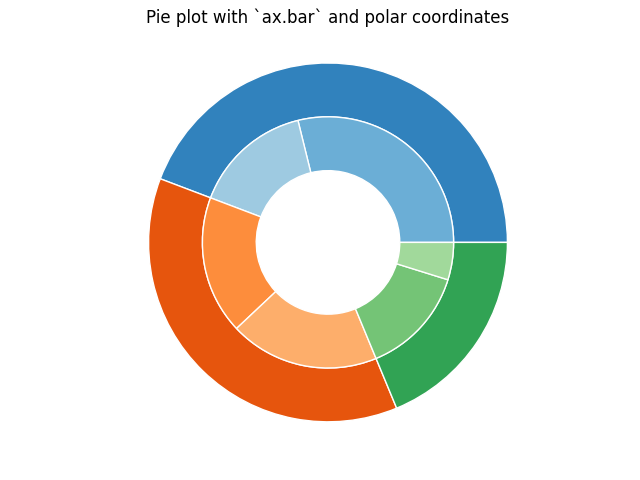
그러나 극좌표계가 있는 축에 막대 그래프를 사용하여 동일한 결과를 얻을 수 있습니다. 이것은 플롯의 정확한 설계에 더 많은 유연성을 제공할 수 있습니다.

이 경우 막대 차트의 x 값을 원의 라디안으로 매핑해야 합니다. 값의 누적 합계는 막대의 가장자리로 사용됩니다.

fig, ax = plt.subplots(subplot_kw=dict(projection="polar"))

size = 0.3
vals = np.array([[60., 32.], [37., 40.], [29., 10.]])
# Normalize vals to 2 pi
valsnorm = vals/np.sum(vals)*2*np.pi
# Obtain the ordinates of the bar edges
valsleft = np.cumsum(np.append(0, valsnorm.flatten()[:-1])).reshape(vals.shape)

cmap = plt.colormaps["tab20c"]
outer_colors = cmap(np.arange(3)*4)
inner_colors = cmap([1, 2, 5, 6, 9, 10])

ax.bar(x=valsleft[:, 0],
       width=valsnorm.sum(axis=1), bottom=1-size, height=size,
       color=outer_colors, edgecolor='w', linewidth=1, align="edge")

ax.bar(x=valsleft.flatten(),
       width=valsnorm.flatten(), bottom=1-2*size, height=size,
       color=inner_colors, edgecolor='w', linewidth=1, align="edge")

ax.set(title="Pie plot with `ax.bar` and polar coordinates")
ax.set_axis_off()
plt.show()

참조

다음 함수, 메서드, 클래스 및 모듈의 사용이 이 예제에 표시됩니다.

Sphinx-Gallery에서 생성한 갤러리