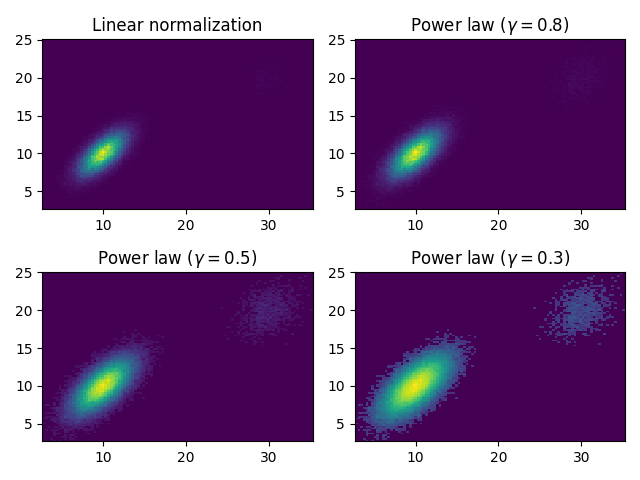
정규화 탐색 #

다변량 정규 분포에 대한 다양한 정규화.

import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import numpy as np
from numpy.random import multivariate_normal


# Fixing random state for reproducibility.
np.random.seed(19680801)

data = np.vstack([
    multivariate_normal([10, 10], [[3, 2], [2, 3]], size=100000),
    multivariate_normal([30, 20], [[3, 1], [1, 3]], size=1000)
])

gammas = [0.8, 0.5, 0.3]

fig, axs = plt.subplots(nrows=2, ncols=2)

axs[0, 0].set_title('Linear normalization')
axs[0, 0].hist2d(data[:, 0], data[:, 1], bins=100)

for ax, gamma in zip(axs.flat[1:], gammas):
    ax.set_title(r'Power law $(\gamma=%1.1f)$' % gamma)
    ax.hist2d(data[:, 0], data[:, 1], bins=100, norm=mcolors.PowerNorm(gamma))

fig.tight_layout()

plt.show()

$선형 정규화, 거듭제곱 법칙 $(\gamma=0.8)$, 거듭제곱 법칙 $(\gamma=0.5)$, 거듭제곱 법칙 $(\gamma=0.3)$$

참조

다음 함수, 메서드, 클래스 및 모듈의 사용이 이 예제에 표시됩니다.

Sphinx-Gallery에서 생성한 갤러리